今天看到一本巨爽的电子书，里面介绍了很多离散几何的神奇结论和美妙证明。我一口气看了将近十个小节，期间不停地被那些天才的数学证明所震撼。电子书的第一节介绍了一个非常初等的东西——Helly定理。从这里大家足以领略到凸集理论的奇妙。
    Helly定理是说，如果一组凸图形中任意三个都有公共区域，那么所有这些凸图形也一定有一个公共区域。注意，这个结论并不是显然的。如果把“任意三个”改为“任意两个”的话结论就不成立了，反例很容易找。另外，“凸图形”这个条件也是必需的——下图中的四块区域满足任意三个都有交集，但它们却没有一块公共的部分。因此，要想证明这个结论，我们必须充分利用“凸图形”这一条件。

    证明对凸集的总个数n施归纳。当n=3时，命题显然成立。不妨来考虑一下n=4的情况。把四个凸集分别记作X_1、X_2、X_3、X_4。我们需要找到一个同属于这四块区域的点。由归纳假设，X_2、X_3、X_4三块区域有一个交集，在这个交集里取一点记为v1；类似地，X_1、X_3、X_4也有一块公共区域，在该区域内选取一点作为v2；用同样的方法确定出v3和v4来。这四个点的位置关系只有两种可能：要么某个点在另外三个点所形成的三角形区域内，要么这四个点构成一个凸四边形的顶点。

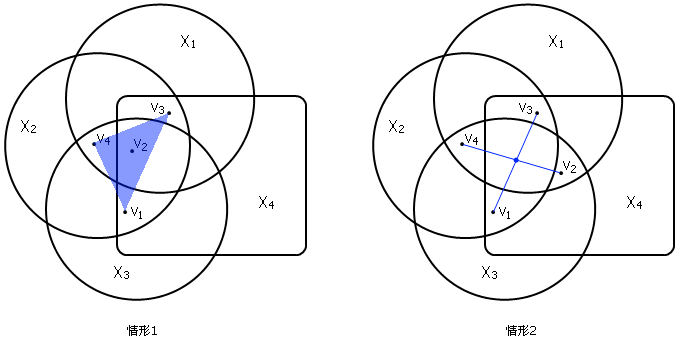
    对于前一种情况，假设v2在v1、v3、v4所形成的三角形区域内。根据我们刚才的构造，v1、v3、v4都在X_2里面，又因为X_2是凸的，因此这三个点所形成的三角形区域也应全部在X_2中；而v2既落在这个三角形中，又位于X_1、X_3、X_4的公共区域内，因此v2就是满足要求的点。对于后一种情况，画出这个凸四边形的对角线，在右图中这两条对角线即为v2v4和v1v3。注意到v1和v3的连线完全落在X_2和X_4的公共区域内，同样地线段v2v4上的所有点都同属于X_1和X_3，因此这两条线段的交点即为所求。因此，无论如何，我总能找到同属于四个凸集的一个点。
    当n再大一些的时候，我们可以仿照上面的做法，在每n-1个凸图形的交集中取一个点。事实上，我们只需要考虑其中的四个点就够了，比如我们就考虑v1、v2、v3、v4四个点。由构造，这四个点全都落在X_5, X_6, …, X_n里面，因此它们的凸包（覆盖这些点的最小凸多边形）也完全位于X_5, X_6, …, X_n的交集内；而前面的分析告诉我们，在这四个点的凸包内存在一个点同属于X_1、X_2、X_3和X_4，于是结论成立。
    事实上，这个结论还可以继续扩展。我们可以证明，对于d维空间中的一组凸集，如果其中任意d+1个凸集的交都非空，那么所有凸集的交非空。这里就不再说了。

 
    Helly定理有一些有趣的推论。其中一个推论是，给定平面上的若干矩形，如果这些矩形的边都与坐标轴平行，并且任意两个矩形都相交，那么所有矩形都会相交。为了证明这个结论，我们只需要说明任意两个矩形相交能推出任意三个矩形相交就行了。考虑任意三个矩形，把它们水平方向上的边投影到x轴上，则我们得到了三条两两之间都有部分重合的线段。由低维的Helly定理，同一直线上的三条线段两两之间都有公共部分，则三条线段必然也有一个公共部分。类似地，三组竖直边在y轴上的投影也有一个公共的部分。因此，事实上这组矩形中任意三个的交都是非空的。
    另一个有趣的结论是，如果平面上的n个点中任意三个都能用一个半径为r的圆覆盖，那么所有这n个点也都能被一个半径为r的圆覆盖。证明这个问题要转一个弯儿：一个圆能覆盖一个点当且仅当圆心离点的距离小于半径。受此启发，分别以这n个点为圆心，做半径为r的圆。于是，题目条件立即变为：刚才作的这n个圆中任意三个都有公共部分。因此，所有这n个圆都有一个公共区域。返回来说，只要把圆盘的圆心放进这个公共区域里，所有n个点都能被这个圆盘覆盖住了。