一条直径可以把圆面积二等分。两条互相垂直的直径可以把圆面积四等分。不过，对于任意的N，将圆面积等分为N个部分并不容易，因为圆周上的N等分点并不总是能用圆规和直尺做出来。1801年，Gauss证明了当n为2的幂和若干Fermat素数的乘积时，正n边形可以用尺规作出图来，同时他猜想这也是必要条件。1837年，Pierre Wantzel证明了这个条件的必要性。第一个无法用尺规完成作图的正多边形是正七边形，也就是说你永远无法仅用直尺和圆规找出圆周上的七等分点。
    不过，这并不意味着我们不能将圆面积分成面积相等的七份。事实上，有一种方法可以将圆分成N个面积相等的部分，其中N可以为任意正整数。你能想到这种方法吗？如果我们还要求各部分周长也相等呢？

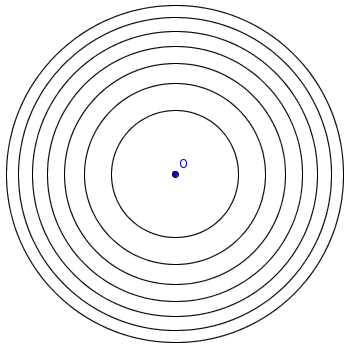
    上图就是一种将圆面积等分为七块的示意图。这些同心圆的半径分别为√1/7, √2/7, …, √6/7。注意这些值都是可以用尺规作出来的。注意两直角边分别为1和√a的直角三角形，斜边为√a+1。从a=1开始出发不断迭代，我们可以依次作出√2、√3、√4等值，再利用相似三角形即可完成除法操作。

 
 
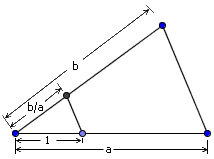
    不过，这个分法并不算一个“正统”的分割方法。如果我们要求每个线条都必需从圆周上出发，并且落脚于圆周上的另一点呢？

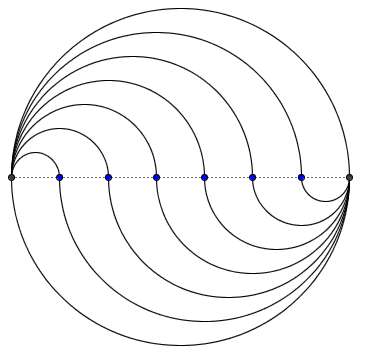
    存在很多等分圆面积的切分方案，但我们却不能用尺规作出来。例如，用N-1根平行的直线总能把圆面积等分为N份，可惜每根直线的位置在哪里需要用到微积分计算，其结果是一个超越方程，无法用尺规作图完成。当然，能用尺规作图完成的分割方法还是有的，不过要想到这种方法并不容易。我们首先作出直径上的七等分点（注意尺规N等分给定线段是可以办到的——可以利用前面的相似三角形做法得到1/N的长度），然后像图中那样依次作出12个半圆弧。做一些简单的计算就可以验证，这些半圆弧形成的七个区域的面积确实是相等的。
    另外，值得一提的是，这个切分方法还有一个神奇的性质：它的每一部分的周长都是相等的。