2009年2月份IBM Ponder This的谜题可能是从98年谜题月赛开办以来最难的谜题。谜题发布一个月之后仍然没有任何人答对，主办人不得不宣布延迟一个月，并再三增加提示。最终，答对此题的仍然只有7个人。很久没有看到如此精彩的谜题了，有兴趣的网友不妨试一试。
    题目非常有趣。传统的谜题是给出谜面求解谜底，但这个谜题则恰恰相反：下面这一串数字是某个问题的答案，你能猜出这个问题是什么吗？这串数字里有一个错误在哪里？

900F 80F0 8F00 80CA BE12 AA90 9400 0048 3E5B 8AC0
3400 00CB BC81 8A08 3C00 0050 BE43 00C0 3E00 A019
8059 BE13 2000 0092 BE9B 2A0B 2A00 8052 8841 04C0
3E00 840B 084B 0098 E000 8819 845A 8012 0300 0050
826F 0500 0600 846E 8264 0900 0A00 8065 0C00 0072
A054 8368 8569 4800 4400 8573 4200 4100 8349 8542
2800 2400 854D 2200 2100 9F00 E000 8888 8444 8000
0030 0DED 8222 0050 0060 8444 8222 0090 00A0 8000
00C0 0DED A000 8333 8555 4080 4040 8555 4020 4010
8333 8555 2080 2040 8555 2020 2010 8300 8500 8030
8050 0880 0840 8050 0820 0810 8030 8050 0480 0440
8050 0420 0410 8500 8030 8050 0280 0240 8050 0220
0210 8030 8050 0180 0140 8050 0120 0110 90F0 9F00
E000 8888 8444 8000 0003 0DED 8222 0005 0006 8444
8222 0009 000A 8000 000C 0DED A000 8333 8555 4008
4004 8555 4002 4001 8333 8555 2008 2004 8555 2002
2001 8300 8500 8003 8005 0808 0804 8005 0802 0801
8003 8005 0408 0404 8005 0402 0401 8500 8003 8005
0208 0204 8005 0202 0201 8003 8005 0108 0104 8005
0102 0101 9F00 8030 8050 8003 8005 0088 0084 8005
0082 0081 8003 8005 0048 0044 8005 0042 0041 8050
8003 8005 0028 0024 8005 0022 0021 8003 8005 0018
0014 8005 0012 0011 80FF 8F0F A333 8000 5000 0DED
8000 3000 0DED A333 C555 1800 1400 C555 1200 1100
8F0F A333 A555 1080 1040 A555 1020 1010 A333 A555
1008 1004 A555 1002 1001

 
 
    答案：首先我们需要把它转成二进制，并绘制一张宽为16像素、高为255像素的位图。在Mathematica里，只需要四句话就可以完成这一系列工作：

st = "900F 80F0 8F00 80CA BE12 AA90 9400 0048 3E5B 8AC0
3400 00CB BC81 8A08 3C00 0050 BE43 00C0 3E00 A019
8059 BE13 2000 0092 BE9B 2A0B 2A00 8052 8841 04C0
3E00 840B 084B 0098 E000 8819 845A 8012 0300 0050
826F 0500 0600 846E 8264 0900 0A00 8065 0C00 0072
A054 8368 8569 4800 4400 8573 4200 4100 8349 8542
2800 2400 854D 2200 2100 9F00 E000 8888 8444 8000
0030 0DED 8222 0050 0060 8444 8222 0090 00A0 8000
00C0 0DED A000 8333 8555 4080 4040 8555 4020 4010
8333 8555 2080 2040 8555 2020 2010 8300 8500 8030
8050 0880 0840 8050 0820 0810 8030 8050 0480 0440
8050 0420 0410 8500 8030 8050 0280 0240 8050 0220
0210 8030 8050 0180 0140 8050 0120 0110 90F0 9F00
E000 8888 8444 8000 0003 0DED 8222 0005 0006 8444
8222 0009 000A 8000 000C 0DED A000 8333 8555 4008
4004 8555 4002 4001 8333 8555 2008 2004 8555 2002
2001 8300 8500 8003 8005 0808 0804 8005 0802 0801
8003 8005 0408 0404 8005 0402 0401 8500 8003 8005
0208 0204 8005 0202 0201 8003 8005 0108 0104 8005
0102 0101 9F00 8030 8050 8003 8005 0088 0084 8005
0082 0081 8003 8005 0048 0044 8005 0042 0041 8050
8003 8005 0028 0024 8005 0022 0021 8003 8005 0018
0014 8005 0012 0011 80FF 8F0F A333 8000 5000 0DED
8000 3000 0DED A333 C555 1800 1400 C555 1200 1100
8F0F A333 A555 1080 1040 A555 1020 1010 A333 A555
1008 1004 A555 1002 1001";
st = StringReplace[st, {" " -> "", "n" -> ""}];
st = IntegerString[FromDigits[st, 16], 2];
ArrayPlot[Map[FromDigits, Partition[Characters[st], 16], {2}]]

    “BRAILLE”是什么？长期订阅本Blog的网友应该不会陌生，Braille点字法是供盲人阅读的凸点文字，我们曾经在另一个谜题中提到过它。Braille点字法比我们想象中的更常用，我有一次就在北京地铁站的扶手上发现了Braille点字。顺着箭头方向看过去，图形右边整齐地分布着一大堆2*3小矩形。这里用到了二级点字，涉及到很多简拼规则，读起来并不容易。

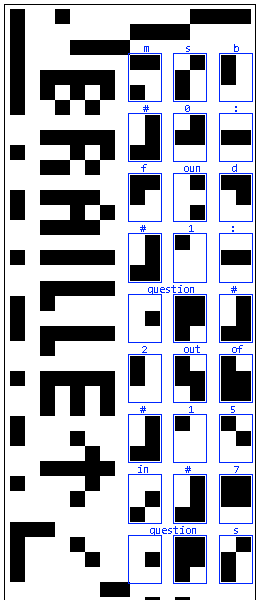
    谜题中隐藏的提示是“msb 0:found 1:question 2 out of 15 in 7 questions”。这句话是什么意思呢？google一下可知，“msb”是“Most Significant Bit”的缩写，表示最高位。根据冒号的位置，我们可以这样理解：当最高位为0时，表示“found”；当最高位为1时，表示“question 2 out of 15 in 7 questions”。用7个问题从15个里面问出两个？这让我们想到一大堆交互式问题。
    事实上，包括上述Braille点字提示在内的所有255个16位整数都是一个交互式问题的解答方案。假设我们有15个球，其中两个有放射性。你需要利用一种放射性检测仪器找出这两个球。每次你可以选取若干个球放入仪器中，仪器会告诉你这些球中有没有具有放射性的球。由于这个仪器十分昂贵，因此你需要用最少的次数来找到这两个球。最少需要多少次操作呢？信息论告诉我们，15个球中有两个放射性球共C(15, 2)=105种情况，7次“是非反馈”能区别2^7=128种情况，因此询问7次已经足够了。这255个16位整数告诉我们应该如何进行询问。这些数按照先序遍历的顺序对所有情况进行编码，例如第一行中1001000000001111表示把第1、2、3、4、13个球放入仪器，余下的所有行中，前一半表示仪器显示没有放射性的情况，后一半就表示有放射性的情况。最高位为0的数都是叶子结点，表示放射性的球已经找到，例如最后一行0001000000000001就表示第1个球和第13个球是放射性的。7次询问只是最坏情况，很多时候我们并不需要7次询问；这就提供了一些插入“废询问”的机会，而这些“废询问”恰好可以用于编写一些提示信息（就是我们先前看到的Braille点字）。不幸的是这个提示信息太长，它所占据的空间超出了“废询问”区间——例如第19个数3E00其实应该是6000，这是为了显示出字母“L”而改的。这就是题目中所说的那一个错误。