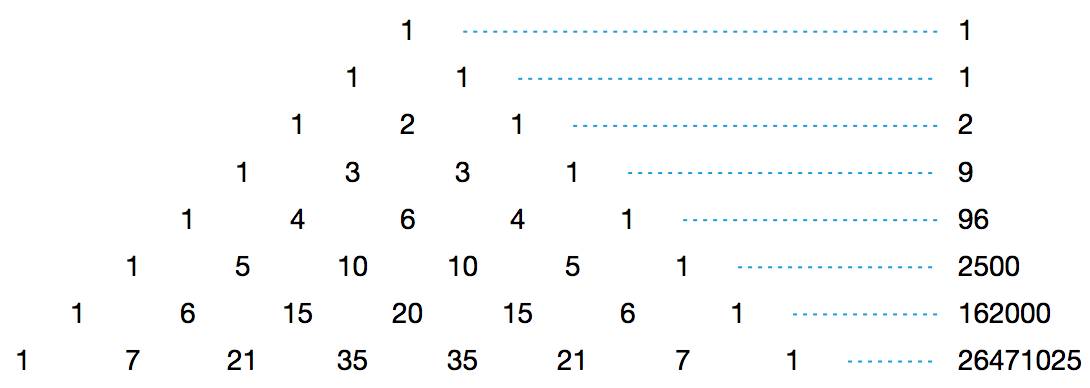
你相信吗，杨辉三角里竟然也有自然底数 e 的身影。 2012 年， Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ，那么随着 n 的增加， sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上，我们有：
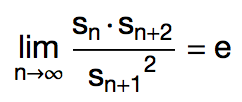
这是为什么呢？ John Baez 在这个网页上给出了一个漂亮的解释。
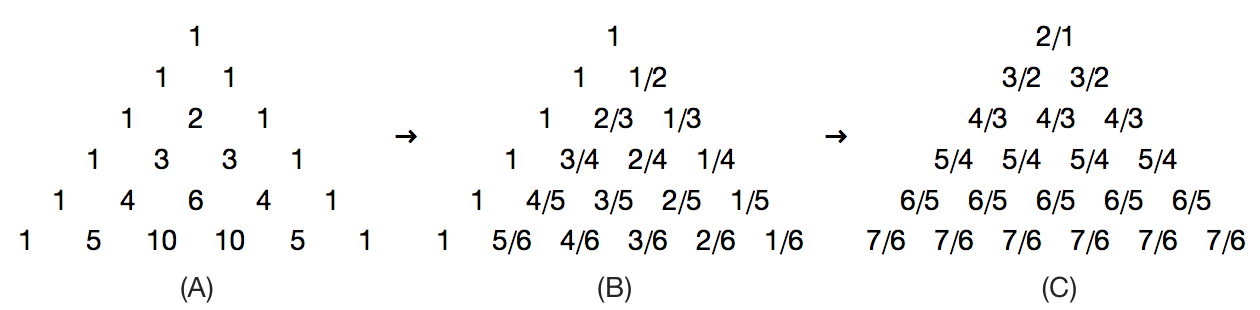
首先，让杨辉三角 (A) 里面的每个数都除以它左下角的那个数，于是得到了图 (B) 所示的三角形数阵。你会发现，这个数阵里有一个很明显的模式，即第 n 行的所有数分母都是 n ，分子则分别是 n, n-1, …, 2, 1 。这并不是巧合。这是因为：
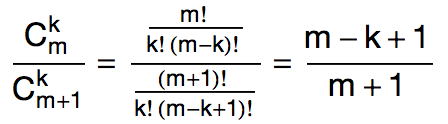
接下来，让图 (B) 里的所有数都除以它右下角的那个数，于是得到了图 (C) 所示的三角形数阵。容易看出，这个数阵第 n 行的所有 n 个数应该都是 (n + 1) / n = 1 + 1/n ，它们乘起来等于 (1 + 1/n)n 。随着 n 的增加，这个数会越来越接近 e 。最后，让我们追溯一下图 (C) 中每个数的来源。图 (C) 中第 n 行的每个数都等于图 (B) 中第 n 行的某个数除以第 n + 1 行的某个数，进而等于图 (A) 中第 n 行的某个数除以第 n + 1 行的某个数的结果，除以第 n + 1 行的某个数除以第 n + 2 行的某个数的结果。因此，图 (C) 中第 n 行的所有数乘起来，结果正是 sn · sn+2 / sn+12
学习了。
组合数相除的表达式的 m 建议用 n，即 C_n^k/C_{n+1}^k。统一符号会更清晰（上下文用的都是 n）。最后几行的解释感觉很别扭（某个数除以某个数再除以某个数，那到底是不是乘上了所有的数？），不如画一个图（再次）演示 n，n+1，n+2 三行的变化。
好巧妙啊，证明简单，能想到这里不易。
终于不是了…
大家能看到那个网页吗？
抢个前排再看……
来学习，博客似乎改版了，清爽了。
Designed by ♥ Localhost
Ant 言之有理，最后一步用文字描述不如用公式；我读最后一段的时候想了很久还是拿出笔和纸来了……设三角数阵（A）中第 n 行所有项之积为An（也就是文中所说的Sn），（B）为Bn，（C）为Cn，那么有：http://i.imgur.com/xvvqHvu.jpg ，所以：http://i.imgur.com/tLv16mE.jpg 得出文中结论。
其中还有一个小细节，那就是三角数阵中第 n+1 行比第 n 行多一个数字，那么怎样保证A→B→C的时候不出现错误呢？A→B的时候数阵两边都是 1 ，除以左下角或右下角都行；而由B→C的时候，要注意全为数字 1 的那边在左在右，在左则除以右下角，在右则除以左下角。
表述比较乱……大家将就看吧。。。
还是原来的样式好:)
虽然不够严谨，但是比高等方法巧多了，只在最后一步用了极限！
再用笔纸验算了一下，其实直接证明（对 C_n^k 连乘的展开）也并不难，John Baez 只是给了一个几何化的较简单解释而已。
为什么手机浏览器看不到了？
很巧妙地证明，感觉就像magic一样，这样一变化立马看到很简单的东西。
巧妙的证明，但可以有更严谨的表达，在做除法那一段，上图不便，楼主忽略。学习了~
我也有一个小小的关于杨辉三角的发现，即：
杨辉三角与素数的神秘关系。
请访问下面链接以获得更多详细内容：
数论中的一个基本原理 闫二斌 西北大学
http://bbs.sciencenet.cn/forum.php?mod=viewthread&tid=1491222&fromuid=1473758
或者我的科学网博客文章：
http://blog.sciencenet.cn/blog-1473758-805555.html
Totally agree, Dale. Watching flash video and listening with flash audio players is a big part of my internet exneriepce. I may still get one because I’m doubtful flash will ever come to iphone or ipad. Still, I’m curious about the HP slate, which has full Windows 7 on it.
长知识了。啊
Nutze Twerfirtitic nicht, lenkt zu stark ab. Ich schau lieber immer mal wieder auf der Seite vorbei, ist effektiver und auch irgendwie spannender, weils immer gleich nen Haufen neuer Tweets sind :>
在实现理想的路途中，必须排除一切干扰，特别是要看清那些美丽的诱惑。