2012-01-27 20:44| 
19 Comments | 本文内容遵从数列 1, 1, 2, 3, 5, 8, 13, 21, 34, … 叫做 Fibonacci 数列。这个数列有很多神奇的性质，其中一个性质是，每一个 Fibonacci 数的平方与它前后两个 Fibonacci 数的乘积一定正好相差 1 。具体地说，如果把第 n 个 Fibonacci 数记做 Fn ，那么有：
Fn+1 · Fn+1 - Fn · Fn+2 = (-1)n
今天看到了这个定理的一个组合数学证明，觉得非常有意思，在这里和大家分享。
Fibonacci 数有很多组合数学上的意义。比如说，用 1 × 1 和 1 × 2 的积木覆盖一个 1 × n 的棋盘，总的方案数恰好是 Fn+1 。下图显示的就是 n 较小时的一些实例：
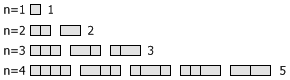
这个规律背后的原因其实很简单：给出一个长度为 n 的棋盘后，它的覆盖方案可以分成两类，最后边放的是一个 1 × 1 的积木，或者最后边放的是一个 1 × 2 的积木。前一类情况下的方案数也就完全取决于前 n - 1 个格子的覆盖方案数，后一类情况下的方案数则等于前 n - 2 个格子的覆盖方案数。因此，如果用 f(n) 来表示 1 × n 棋盘的覆盖方案数，那么正好就有 f(n) = f(n - 1) + f(n - 2) 。另外，由于 f(1) = 1 ， f(2) = 2 ，因而接下来的数 f(3), f(4), f(5), … 也就恰好构成了 Fibonacci 数列。
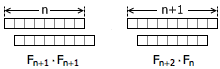
既然这样，那么用积木覆盖两个独立的 1 × n 棋盘，总方案数就是 Fn+1 · Fn+1 。我们有意把这两个独立的棋盘像左图那样摆放。类似地，用积木覆盖一个 1 × (n+1) 棋盘加上另一个 1 × (n-1) 棋盘的总方案数则为 Fn · Fn+2 ，我们把这两个棋盘放成右图所示的样子。左图的覆盖方案和右图的覆盖方案之间有一种非常巧妙的一一对应关系。
对于左图中的任意一种覆盖方案，我们找出上下两块棋盘中所有位置重合的“公共分割线”，选出最右边的那条公共分割线，然后交换此分割线右侧的部分。这样，左图棋盘的每个覆盖方案就能变成右图棋盘的一个覆盖方案。根据同样的方法，右图棋盘的每个覆盖方案也能变回左图棋盘的覆盖方案，这就说明了 Fn+1 · Fn+1 和 Fn · Fn+2 是相当的。
等等，那为什么当 n 为偶数时， Fn+1 · Fn+1 比 Fn · Fn+2 要大 1 ，而 n 为奇数时， Fn+1 · Fn+1 会比 Fn · Fn+2 小 1 呢？神就神在这里。这是因为，刚才所说的一一对应关系并不是真的完全一一对应的。当 n 为偶数时，左图棋盘有一例极其特殊的覆盖方案无法对应到右图的棋盘——因为这种方案中根本没有公共分割线。当 n 为奇数时，左图的棋盘就不再有如此特殊的覆盖方案了，但右图棋盘中却又多出了一例没有公共分割线的情况。这就证明了 Fn+1 · Fn+1 - Fn · Fn+2 = (-1)n 。
哈哈，组合论证总是绝妙的，精彩啊。
木有沙发
想要严谨点，就还要证明没有其它的极端情况。怎么办？
同意exp618,证明其他情况刚好能够找到“公共分割线”是必要的。
似乎，那个证明也挺有趣的。
沙发早就没了。。。
还是数学归纳法更轻松直接……
前排
前排
地核下面好像就是10层了……
@exp618：只需注意到铺砌中存在1x1方块时必然存在公共分割线。
@地壳 不带这么玩的。
这个证明方式跟《编程之美》上买票找零中 面额100 50的有效排列方式是相同的，用于卡特兰数公式的推导
挺巧妙地
= =总觉得某个IMO预选题和这个类似来着...
组合数学一直是我的硬伤啊
感觉最后一段似乎关键点是那个分割线，如果没想到有这么个“分割线”的话，可能就不会说出这一句“因为这种方案中根本没有公共分割线”了。 能不能说下你是怎么想到这个“关键的分割线”的？
最近正好想写一篇有关斐波那契数列通项求法的、仅用高中生水平知识的博文，很兴高采烈地点了进来……结果，并非通项的讨论，稍稍失望……
顺便借地问问，斐波那契数列通项的某推导法，某步使用了“可将斐波那契数列拆成两个等比数列的和”貌似依据高中数学中的特征方程算得——但，凭什么判定该数列能这般拆呢？求教