Lee Sallows 最近做了一个网站,收集了很多在几何意义上也成立的幻方,集数学与艺术于一体,为传统意义的幻方赋予了新的生命。大家来欣赏一下吧。
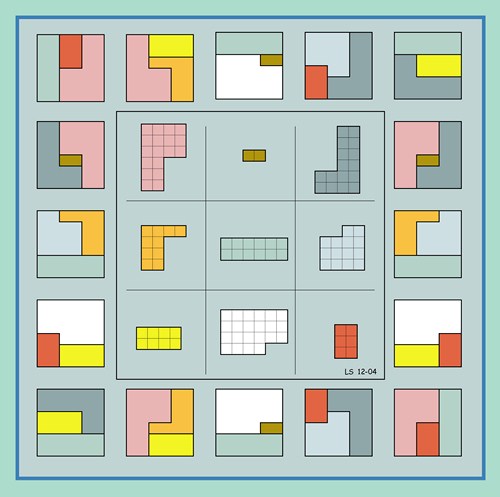
这是一个幻方,它由九块积木组成。这些积木所含的小方格数分别是 2, 6, 8, 10, 12, 14, 16, 18, 22,每行每列和两对角线上的方格总数都是 36 。 牛 B 的是,每条线上的三块积木正好也都能拼成一个 6 × 6 的矩形。
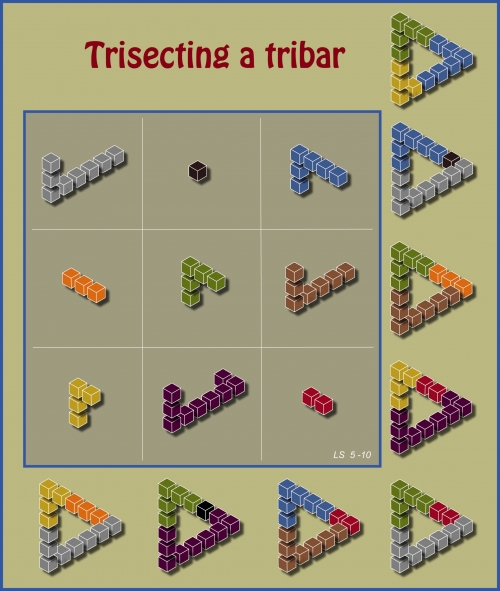
与上图类似的一个几何幻方,不过明显更帅一些。

这个可以说是三重幻方了:幻方中的积木所含的小方格数恰好是前 9 个正整数,并且每条线上的三块积木正好能拼成一个(中间带有空洞的)正方形,而这些 4 × 4 的正方形本身又构成了幻方(空洞代表零)。
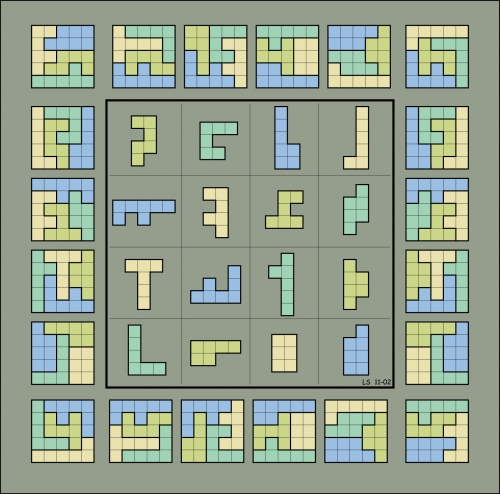
当然,四阶也是有的。这就是一个四阶的几何幻方。

这是一个更牛的四阶几何幻方。不但每条线上的四块积木都能拼出 5 × 5 的方形,而且积木里书写的数字加起来也都是 44 。

这是另一个四阶几何幻方。中间是由 16 块图形组成的,它们大致排成了 4 × 4 的形状。这 16 块图形本身就组成了四个正方形,而每行每列和两条对角线上的四块图形也都能拼成正方形。

这是一个不是幻方的几何“幻方”。平面上有九个圆圈,它们排成了九行,每行三个圆圈。每个圆圈里有一种积木。每条线上的三块积木,以及每个等边三角形三个顶点上的积木,都能拼成同一个图形。