最近在做网站测试时，遇到了需要在输入框输入 3000 字的测试用例。联想到平时聊天时经常复制粘贴一堆笑脸刷屏讨 MM 欢心的行为，不由想到了一个有趣的问题：为了输入一定数量的字符，最少需要按多少个键？
大家最常用的策略或许是， 先输一些字符，然后全选复制，粘贴到一定规模后，再全选复制，粘贴到一个新的数量级，如此反复。注意到进入全选状态（并且复制后），第一次粘贴将会覆盖掉选中的部分，第二次粘贴才会增加原来的文本长度。当然，全选复制后按一次向右键也可以消除选中状态，不过却并没有节省按键次数。因此我们规定，在输入字符时只有四种原子操作：
1. 按一个按键，输入一个字符
2. 按 Ctrl + A ，全选
3. 按 Ctrl + C ，复制
4. 按 Ctrl + V ，粘贴
排除明显不划算的行为，真正的决策其实只有两种：
1. 按一次按键，输入一个字符
2. 按 k + 2 次按键，将现有内容复制成 k 份。
这样一来，我们就有了一个清晰的递推思路。设 f(n) 表示输入 n 个字符所需要的最少按键次数，则 f(n) 将会在 f(n-1) + 1 和 f(n/k) + k + 2 中取一个最小值（其中 k 取遍 n 的所有约数）。
Mathematica 牛 B 就牛 B 在，这样的动态规划程序只需要一行便能写完：
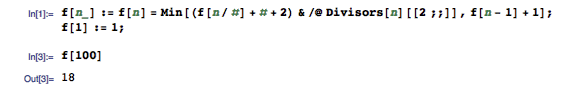
可见，输入 100 个字符需要 18 次按键。具体方法是，用 5 次按键输入 5 个字符，再用 7 次按键把它变成 25 个字符，再用 6 次按键把它变成 100 个字符。
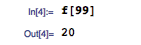
有趣的是，这个函数并不是单调的。输入 99 个字符需要的按键次数比输入 100 个字符需要的按键次数更多一些，事实上这最少要花费 20 次按键。方法是，先用 5 次按键输入 5 个字符，4 次按键把它变成 10 个字符，单独按一次键添加一个字符， 5 次按键把字符数复制粘贴到 33 ，再来 5 次按键把字符数复制粘贴到 99 。
下面这个图是输入不同的字符数所需要的最少按键。
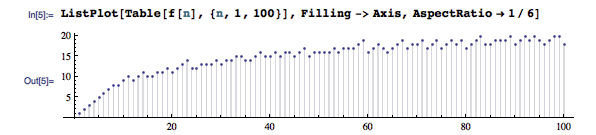
可以看到， 20 次按键足以应付 100 以内任何数量的字符，也就是说 99 个字符所需要的按键次数已经是 100 个字符以内的情况中最大的了。不过，最悲剧的应该要数 83 个字符了，它是所有至少要用 20 次按键的情况中字符个数最少的（也即首次出现的要用 20 次按键才能输入的情况）。对应的输入方案是 5 → 20 → 80 → 81 → 82 → 83 （直到分析到这里，我才意识到，在考虑输入指定数量的字符时，引入退格键可以带来的更少的按键次数）。
那么， 20 次按键最多可以输入多少个字符呢？为了解决这个问题，我们可以给出另外一个递推式。令 g(n) 为 n 次按键最多可以输入的字符个数。对于每一个 n ，考虑两种转移决策：要么在 n – 1 次按键能够达到的最大字符数基础上加 1 ，要么把 n – k 次按键能够达到的字符数复制成 k – 2 份。也就是说， g(n) 就等于 g(n-1) + 1 和 g(n-k) * (k-2) 的最大值，其中 k 可以从 3 取到 n – 1。我们还是用一句话写下这个转移方程式：
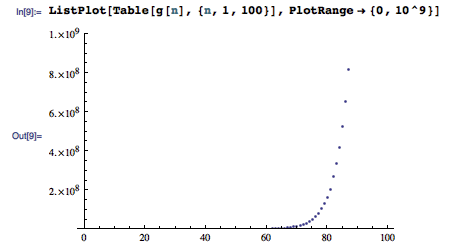
可以看到， 20 次按键足以输入 150 个字符（方案是 6 → 30 → 150 ）， 30 次按键足以输入 1600 个字符（方案是 5 → 25 → 100 → 400 → 1600 ）。这样看上去，我们好像有了快速刷屏的指导思想：粘贴到原来的 4 倍长或者 5 倍长后再进行下一波全选复制粘贴似乎总是最优的选择。另外，这个数列增长得很快， 80 次按键能输入的字符数就已经上亿了。看来，要想刷屏到系统崩溃并不难，不足 100 次按键就能产生上 G 的数据。
似乎这个增长速度是指数级的。描出 g(n) 的图象证实了我们这一想法：
我们自然而然地想到观察数列 g(n) 相邻两项的比值：
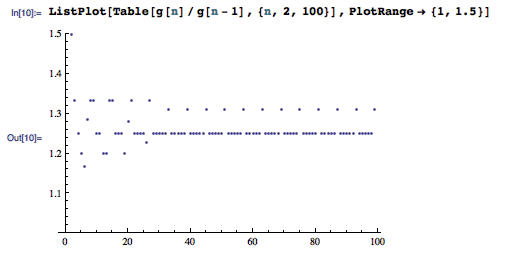
容易看到，当 n 到了一定大时，数列已经呈现出了一定的规律，多数时候都是以 1.25 倍的速度增长。给出并证明数列的通项公式或许会是一件非常有趣的事情。
沙发？
板凳？
以前我也考虑过这个问题，不过还是Matrix同学更深入啊
前排?
跟将一个数拆分成若干个数之和，怎么拆分能得到最大的乘积，有点类似。
对于足够大的n，根据观察有g[6n-2]=2^2n, g[6n-1]=2^(2n-2)*5, g[6n]=2^(2n-4)*5^2, g[6n+1]=2^(2n-6)*5^3, g[6n+2]=2^(2n-8)*5^4, g[6n+3]=2^(2n-10)*5^5。应该容易证明这个规律是对的，因为形式什么的很简单。一旦成立了指数增长，每次最优的k应该是固定的。
我的蛋…
但是你这是基于按键次数的……
实际中复制操作都会利用自动重复……是基于时间的……
另外也没有考虑到可以设定按键映射的情况……
map m axxxxxggVGyGpG
地核？
输入99个字符可以先输入100个字符，然后按Backspace键
我已经不疼了，我的已经碎了……
使用预先设定的macro可以快很多
很有意思的一篇文章.
楼主忽略了两个问题，而这对于严谨的数学推导来说是不能忽略的。
1。Ctrl-V 是两个按键，而不是一个按键。
2。当第一次按 Ctrl-V 的时候是两个按键，连续按两次的时候，按键次数又不同了，如果使用连击，则又不相同。
蹉 为什么我每篇都看不懂 我还每次都来这。。。。。。。。。。。
楼主可以考虑单位时间内的最优方法- -。
按下键盘后的重复时间是不同的。比如我这里按下键盘立刻就开始重复字母。但是从ctrlA到ctrlC切换却是要时间的。
博主嫌难题不够多特地送来的证明题… <_<
同样道理，Ctrl-A, Ctrl-C, Ctrl-V 是六个按键，而不是三个。
看来DT也不错
这题的本质是信息熵
大牛能不能解释下In[1]里的那个[2;;]什么意思
为何不能先打出k个字符再进行删除？
确实可以 打99个字符只需要先打100个再删一个 仅需要19次按键
如果考虑到退格箭 原先的函数图像是不是会变得更美观？即相邻两数字所需按键数最多只会差一次
如果考虑到退格键 原先的函数图像是不是会变得更美观？即相邻两数字所需按键数最多只会差一次
现在一般都是用图刷屏,效率高- –
回复22楼。mathematica里的意思是从2开始，固定的这样写
我一般都是输入几个字，Ctrl+C 一次 / Ctrl+V 几次，然后再 Ctrl+C 一次 / Ctrl+V 几次——长按Ctrl+V，就可以不停的粘贴粘贴粘贴，速度取决于键盘的反应速度。
Ctrl+C 到 Ctrl+V 之间是要切换时间的，如我前面的某回复所言——而且，多累啊。长按Ctrl+V才是王道。
1. 按一个按键，输入一个字符
2. 按 Ctrl + A ，全选
3. 按 Ctrl + C ，复制
4. 按 Ctrl + V ，粘贴
123442344234423442344, 2^n 增长
如果要算超过255的，比方说1000的，Mathematica还牛么？
哈哈，这也是我曾经研究过的东东！
this is one of the hottest questions on stackoverflow…
http://stackoverflow.com/questions/4606984/maximum-number-of-characters-using-keystrokes-a-ctrla-ctrlc-and-ctrlv
做过一道类似的题目：一个计算器有两个存储器x1,x2,一开始x1=1,x2=0,一次操作可以：将【x1或x2或（x1与x2的和或积或大数减小数的差）】存入x1或x2,或者输出x1或x2。对于需要输出的任意一个正整数，输出最小操作次数。当时动归写爆了。。
写了一个haskell的代码计算上面的g函数，应该还可以更短的吧。
ghci> let arr = array (0,len) $ [(0,0), (1,1), (2,2)] ++ [(n, max (arr ! (n-1) + 1) $ maximum $ map (m -> (n-m-2) * arr ! m) [1..n-2]) | n arr ! 100
17179869184
代码提交之后变化了，重贴一下
let arr = array (0,len) $ [(0,0), (1,1), (2,2)] ++ [(n, max (arr ! (n-1) + 1) $ maximum $ map (m -> (n-m-2) * arr ! m) [1..n-2]) | n <- [3..len]] ; len = 10000
很给力，这个问题我曾经也想过，不过用的方法不够科学，是通过人为计时的方法，看看30秒内，怎么样刷最多，当然这样一来刷屏的方法需要人手操作，熟练度不行的话，操作一复杂就会乱套，也就是说实际上复制个多次反而不如相对简单的复制一两次来的快，哈哈，毕竟人会按错键，会脑抽。。已转载至http://blog.163.com/nyningyu@126/blog/static/120265575201111102745685/
SPOJ上有道题吧。。。
-.-
发现灰雁- –
ctrl+a
ctrl+c
->
ctrl+v
长度变为3倍…
话说这个问题我也想过.
应该是用二分逆运算来做,但问题是,前几次的输入怎样保证用尽量少的按键按出尽量多的字母…
哈哈，刷屏不会说一定要刷多少字，所以一直按就行了。这不光是一个数学的问题。还有惯性的问题，因为在操作上，不停的按10次ctrl+v，要比按5次ctrl+a ctrl+v要快得多。
单从数学方面来说，可不可以简单的看成，公约数越多的数，输入得越快呢。
其实这可以就像ijos上的一道水题。。
嗯。。我也eggache地这么粘贴过“对不起”
刷频这道有些难倒我了！
说“打99个字符只需要先打100个再删一个”的都是没仔细读文章的，原文括号中有一句话：
（直到分析到这里，我才意识到，在考虑输入指定数量的字符时，引入退格键可以带来的更少的按键次数）
開個玩笑：
vim x.txt
800iGoto hell! (esc)
ZZ
open x.txt
刷频这道有些难倒我了！
我无耻地看懂了，MD
其实，你可以用鼠标复制粘贴的^o^
0:
1:
#,
2:
#, #,
3:
#, #, #,
4:
#, #, #, #,
5:
#, #, #, #, #,
6:
#, #, #, #, #, #,
7:
#, #, #, #, #, #, #,
8:
#, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V,
9:
#, #, #, Ctrl + A, Ctrl + C, 3 * Ctrl + V,
10:
#, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V,
11:
#, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V, #,
12:
#, #, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V,
13:
#, #, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V, #,
14:
#, #, Ctrl + A, Ctrl + C, 7 * Ctrl + V,
15:
#, #, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V,
16:
#, #, #, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V,
17:
#, #, #, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V, #,
18:
#, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V,
19:
#, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V, #,
20:
#, #, #, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V,
21:
#, #, #, Ctrl + A, Ctrl + C, 7 * Ctrl + V,
22:
#, #, #, Ctrl + A, Ctrl + C, 7 * Ctrl + V, #,
23:
#, #, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V, Bksp,
24:
#, #, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V,
25:
#, #, #, #, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V,
26:
#, #, #, #, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V, #,
27:
#, #, #, Ctrl + A, Ctrl + C, 3 * Ctrl + V, Ctrl + A, Ctrl + C, 3 * Ctrl + V,
28:
#, #, #, #, Ctrl + A, Ctrl + C, 7 * Ctrl + V,
29:
#, #, #, #, Ctrl + A, Ctrl + C, 7 * Ctrl + V, #,
30:
#, #, #, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V,
31:
#, #, #, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V, #,
32:
#, #, #, #, Ctrl + A, Ctrl + C, 8 * Ctrl + V,
33:
#, #, Ctrl + A, Ctrl + C, 5 * Ctrl + V, #, Ctrl + A, Ctrl + C, 3 * Ctrl + V,
34:
#, #, #, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V, #, Ctrl + A, Ctrl + C, 2 * Ctrl + V,
35:
#, #, #, #, #, Ctrl + A, Ctrl + C, 7 * Ctrl + V,
36:
#, #, #, #, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V,
37:
#, #, #, #, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V, #,
38:
#, #, #, Ctrl + A, Ctrl + C, 6 * Ctrl + V, #, Ctrl + A, Ctrl + C, 2 * Ctrl + V,
39:
#, #, #, Ctrl + A, Ctrl + C, 4 * Ctrl + V, #, Ctrl + A, Ctrl + C, 3 * Ctrl + V,
40:
#, #, #, #, #, Ctrl + A, Ctrl + C, 8 * Ctrl + V,
带backspace
《论如何用最少的步数在文档中仅用键盘输入n个‘#’号》