趣题：三角形内切圆的一个性质

  

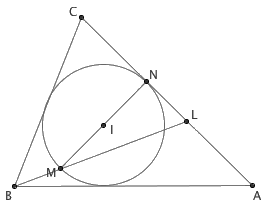
    动脑时间咯！搞搞几何题，脑子不生锈。作出任意三角形 ABC 的内切圆 ⊙I ，它与 AC 相切于点 N 。过 N 作 AC 的垂线，与 ⊙I 的另一个交点记作 M （因此 MN 就是这个圆的一条直径）。连接并延长 BM ，与 AC 交于点 L 。求证： CN＝AL 。

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
  

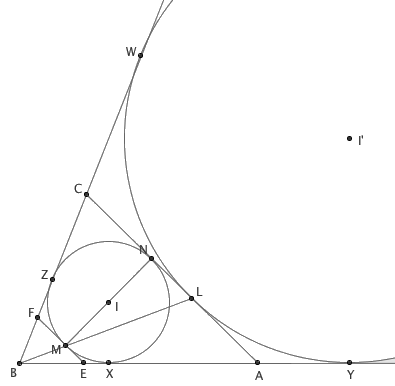
    下面这个证明方法很妙：过 M 点作 ⊙I 的切线，与 AB 、 BC 分别交于点 E 、 F 。因此， EF 与 AC 平行。以 B 点为中心，把 △BEF 放大到 △BAC ，则 M 点就会和 L 点重合，而 ⊙I （作为 △BEF 的旁切圆）则会变成 △BAC 的旁切圆 ⊙I’ 。
    下面我们要用到与切线长相关的两个定理：

      (1) 两圆的两条外公切线等长
      (2) 圆外一点到圆的两条切线等长

    由 (1) 可知 XY = ZW ，即 AX + AY = CZ + CW 。由 (2) 可知 AX 、 AY 、 CZ 、 CW 分别等于 AN 、 AL 、 CN 、 CL 。于是有 AN + AL = CN + CL 。等式两边都减去 NL 一段，有 2 * AL = 2 * CN ，结论就证到了。

问题来源：http://www.cut-the-knot.org/Curriculum/Geometry/PerpIndiameter.shtml

37 条评论

回复给 P.K. 取消回复

8  ×  1  =