玩转内接多边形（五）：任意多边形内均存在内接菱形

我们曾经用两种巧妙的方法证明了这样一个命题：任意凸多边形内均存在内接菱形。利用上次讲到的登山引理，我们可以证明一个更强的命题：任意多边形内均存在内接菱形。

证明的大致思路如下：在多边形外任选一点 u 。把多边形上离 u 最近的点记作 y ，把多边形上离 u 最远的点记作 z 。 y 和 z 这两个点就把整个多边形的边界分成了两个部分。

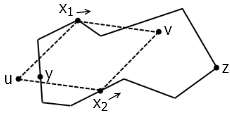
回忆登山引理的内容：对于两个函数值从 0 连续地变到 1 的“折线段函数” f(x) 和 g(x) ，我们总能连续地调整 x1 和 x2 的位置，使得 f(x1) 与 g(x2) 总保持相等，它们从一开始的 0 出发，同时到达 1 。把登山引理应用到上图中，我们可以得到这个结论：我们可以让点 x1 从 y 出发沿着图中的上半部分移动到 z ，点 x2 从 y 出发沿着图中的下半部分移动到 z ，并且保证 x1 到 u 的距离始终等于 x2 到 u 的距离（为了照顾对方，必要时 x1 和 x2 可能会走回头路）。这样， u 、 x1 、 x2 就始终能成为一个菱形的三个顶点。我们把菱形的第四个顶点记作 v 。容易证明 v 的轨迹也是连续的。
当 x1 和 x2 离 y 点充分近的时候， v 点显然在多边形内部；但当 x1 和 x2 跑到 z 附近时， v 显然就跑到了多边形外。在此过程中， v 点必然穿过了多边形的边界，此时 u 、 x1 、 x2 、 v 就构成了这样一个菱形，它的后面三个顶点都在多边形上。

现在，固定 y 点，让 v 点逐渐靠拢 y 点，则对应的这个菱形也会连续地发生变化。容易想到，这一过程的极限将会收敛到某个固定的菱形（这是可以证明的），它就是我们所求的内接菱形。

13 条评论