大家都知道，我们永远不可能尺规三等分任意角。借助一些其它的工具是可以办到的，即使所借助的东西“微不足道”，“几乎可以不算”。下面提供四种比较简单的方法。


ONE~~~~~~~~~
    至今仍有不少人认为这种方法可以推翻“三等分角不可能”的结论。而事实上，这种方法仍然算借用了外物。
    尺规不能三等分角，但可以三等分圆（自己试）。也就是说，只用直尺和圆规可以画出120度的角来。现在给你一个任意角，那么你可以把它对应的扇形卷成一个圆锥，三等分这个圆锥底面的圆。还原成扇形后，你会看到这个角所对应的圆弧已经被平分为三份了。



TWO~~~~~~~~~
      
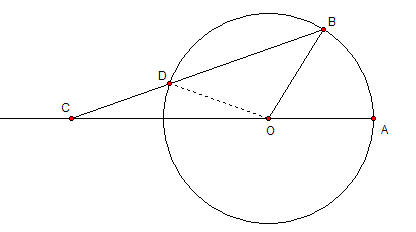
    把要三等分的角AOB放在圆中，作为圆心角。从B出发作射线交圆于D，交AO延长线于C，当CD等于圆的半径时角ACB就是角AOB的1/3。你可以试着自己证明一下。
    证明：设∠DCO=x。由CD=DO知∠DCO=∠DOC，于是∠DOC=x，进而∠BDO=2x。由DO=BO知∠BDO=∠DBO，于是∠DBO=2x，进而∠AOB=∠ACB+∠DBO=3x。
    结论是正确的，可惜如果不在尺子上作标记的话图是作不出来的。



THREE~~~~~~~
      
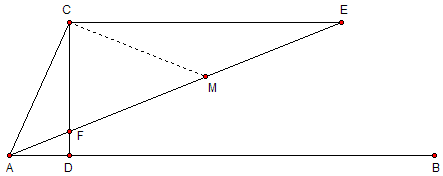
    我们要三等分角BAC。作CD垂直于AB，垂足为D。作CE平行于AB。AE交CD于F。适当移动E的位置（仍然保持CE//AB），当EF=2AC时，∠EAB=1/3∠CAB。
    证明很简单：找出EF的中点后，于是EM=FM=CM=AC，那么∠CAM=∠CMA=2∠AEC，又因为CE//AB，所以最终可得∠CAE=2∠EAB，也即∠EAB=1/3∠CAB。和方法二一样，尺子上面没有刻度的话是作不出这个图的。



FOUR~~~~~~~~
      
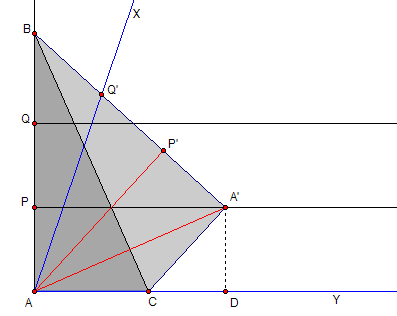
    如果你手上有一张纸的话，你可以用折纸的方法三等分角。
    把角XAY（蓝色标明）放在纸的一个直角上，AY靠着纸的边缘。在纸的另一直角边上确定两点P和Q使得AP=PQ，过这两个点分别作平行于AY的直线。现在，把纸折起来，让Q点落在AX上，A点落在过P的那条平行线上，那么A和P的落点就确定了三等分线的位置（红色线段）。怎么证明呢？
    证明：为了便于叙述，我们把A、P、Q的落点分别命名为A'、P'、Q'，折痕的端点分别为B和C。过A'作A'D垂直于AY。∠AA'D = 90°- ∠A'AD = ∠BAA'。又AB=A'B，于是∠BAA'=∠BA'A。加上A'D=PA=P'A'，AA'是公共边，足以说明△AA'P'≌△AA'D (SAS)。这样，∠AP'A'和∠AP'Q'都是直角。又注意到AP=PQ即A'P'=P'Q'，于是△AP'A'≌△AP'Q'。以A为顶点的三个直角三角形全等，也即对应的三个角相等。

做人要厚道
转贴请注明出处