1956年Robert Abbott发明了一个全新的纸牌游戏叫做Eleusis,后来Martin Gardner在1959年6月的Scientific American杂志上介绍了这个游戏。77年10月这个游戏又进一步得到完善,并发展出一些其它的玩法。最近,John Golden提出了这个游戏的第三个版本Eleusis Express,他比Eleusis更简单,更完备,平均游戏时间也更短。Robert Abbott对这个游戏非常满意,这种简单而有趣的推理游戏很可能会像杀人游戏一样流行起来。下面我简单介绍一下这个游戏的规则,你将会看到一种集策略和推理于一体的全新的纸牌游戏。
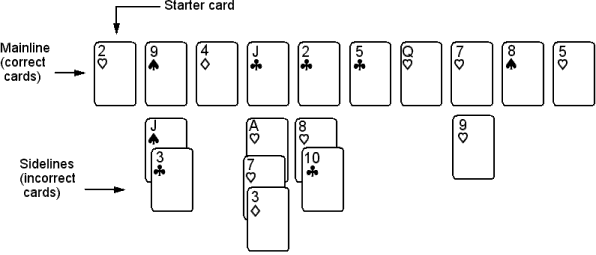
这个游戏的规则极其简单,但变化也异常丰富,因为这个游戏的出牌方式是不固定的,游戏开始时玩家甚至不知道出牌的规则是什么。玩家的主要任务就是在游戏过程中探索出牌的规则。游戏需要两副牌,玩家以3到8人为宜。每轮游戏前,玩家需要推选出一位主持人,主持人在这个游戏里扮演最重要的角色。游戏开始前,主持人自己在心里默想一个出牌规则(Secret Rule),但不能告诉玩家。规则的内容应该只考虑扑克牌的花色与点数,与出牌人、牌的摆放方式等无关。这个规则必须简单、明确,通常以“如果上一张牌是什么什么,那么下一张牌就该接什么什么”一类的形式给出,比如“如果上一张牌是红色,下一张牌就是黑色;如果上一张牌是黑色,下一张牌就该是红色”,或者是“要么与前一张牌同花色,要么与前一张牌同点数”。然后主持人洗牌,给每个人发12张牌,然后再翻出一张放在桌面上作为第一张牌打出。这张牌及后面正确的跟牌都摆成一行,叫做主线(Mainline);主线下方可能会有若干边线(Sideline),表示错误的跟牌。游戏正式开始前,主持人可以对秘密规则进行一些提示,之后玩家轮流打牌,主持人判断玩家打出的牌是否符合他的规则:
如果打出的牌符合规则
此时主持人把这张牌加在主线的右边,该玩家手中的牌就少了一张。如果此时该玩家手中的牌打完了,则游戏结束,否则游戏继续进行。
另外,该玩家还可以获得一次猜测出牌规则的机会,同时每个玩家都必须听他说的答案。如果该玩家猜对了,主持人也宣布游戏结束,否则游戏继续。
如果打出的牌不符合规则
此时主持人把这张牌放在的相应的边线位置上,告诉大家这张牌不能接在这个位置。这名玩家需要再摸一张牌,手中的牌的张数不变。
轮到某位玩家出牌时,该玩家可以选择不出牌,即宣称自己无牌可打。此时他应该把手中的牌摊出来给所有人看,同时主持人判定该玩家是否确实无牌可打:
如果该玩家确实无牌可打
如果此时玩家手中只有一张牌,游戏结束。否则,主持人清点该玩家手中牌的数目N,把它们放回还没发完的牌摞的最底下,再发给他N-1张牌。同时,该玩家获得一次猜测出牌规则的机会,猜对了同样可以直接获胜。
如果该玩家有可以打的牌
此时主持人从中选出一张可以打的牌接在主线后面,该玩家收起自己其余的牌并再摸一张,保持手中的牌数不变。
游戏结束后,每个人的得分就是自己打出去的牌的张数。打完所有牌而获胜的玩家再获3分的加分,猜对规则而获胜则得到6分的加分。主持人的得分与本轮最高分相同。然后大家重新推选主持人,继续下一轮游戏。
如果牌抓完了但游戏还没结束,可以再洗一副牌继续进行,或宣布游戏结束,本轮不计分。然后,主持人阴笑几下,故弄玄虚地说出自己所想的规则,等待玩家们恍然大悟并集体发出“哎呀~~~”的叹息声(或者等待玩家大骂这规则太他妈BT了谁能想到啊)。
若干轮游戏后,最终的胜者就是累积得分最高的人。我们可以适当给赢家一些奖励,比如让他亲一下最漂亮的MM玩家,或者传几个小A给他。得分最低的人也应当受到惩罚,比如叫他把MM共享出来让大家玩弄,或者贡献一个XX论坛的账号。
能想到一个简单明了而又富有新意的规则是非常重要的,因此游戏的主持人是整个游戏的灵魂,一个思维活跃又爱捉弄人的主持人可以让游戏变得非常精彩。这里写一些自己想到的规则,大家有什么好的想法也可以在下面说一说。
- 按黑红梅方的顺序出牌
- 按三张红色,三张黑色,又三张红色,又三张黑色的顺序出牌
- 如果上一张牌的点数是1到7,则应该接8到K;如果上一张牌是8到K,则应该接1-7
- 相邻两张牌的点数之和大于10
- 相邻两张牌的点数的差的绝对值不超过3
- 相邻两张牌的点数加起来能被3整除
- 下一张牌的点数比上一张牌大1点、2点、3点或4点;数字大小关系是“循环的”
- 如果上一张牌的点数是奇数,则出红色牌;如果上一张牌的点数是偶数,则出黑色牌
- 如果上一张牌是红色,则出牌的点数小于等于上张牌的点数;否则,出牌的点数大于等于上张牌的点数
- 如果上一张牌的点数为平方数,则出牌的点数是非完全平方数;否则出牌的点数应该是一个平方数
- 牌的点数一大一小交替排列(即奇数位置上的牌比前面的点数小,偶数位置上的牌比前面点数大)
- 如果花色与前面一张相同,则点数必须比它大;如果花色与前面一张不同,则点数必须比它小
做人要厚道 转贴请注明出处
查看更多:http://www.logicmazes.com/games/eleusis/index.html