大家或许都听说过一个与正方形剖分相关的非常经典的问题:对于哪些正整数 n ,我们可以把一个正方形分割成 n 个小正方形(允许出现大小相同的小正方形)?答案是,除了 n = 2, 3, 5 以外,对于其他所有的 n ,把一个正方形分割成 n 个小正方形都是有可能的。对于 n = 1, 4, 6, 7, 8 的情况,分割方案如下图所示:
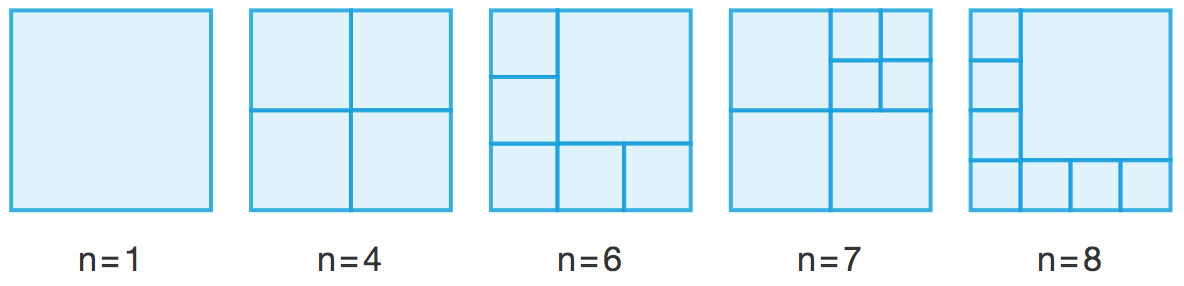
对于更大的 n 呢?注意到,每次用横竖两条线把一个小正方形分成四个更小的小正方形后,我们都会让这个图形里的正方形数目增加 3 个。因此,我们只需要在 n = 6 的方案上增加两笔,就能得到一个 n = 9 的方案;只需要在 n = 7 的方案上增加两笔,就能得到一个 n = 10 的方案;只需要在 n = 8 的方案上增加两笔,就能得到一个 n = 11 的方案;只需要在 n = 9 的方案上增加两笔,就能得到一个 n = 12 的方案……于是,其他所有的情况都被我们解决了。
不过,你有没有想过,同样的问题搬到立方体上,答案又会如何呢?换句话说,对于哪些正整数 n ,我们可以把一个立方体分割成 n 个小立方体(允许出现大小相同的小立方体)?人们已经证明了一个和刚才类似的结论:除了有限多个 n 以外,对于其他所有的 n ,这个问题都是有解的。事实上,对于所有的正整数 n ≥ 48 ,把一个立方体分割成 n 个小立方体都是有可能的。
证明思路和刚才一样。在任意一种立方体剖分方案中,每次把一个小立方体分割成 8 个更小的立方体,整个剖分方案中的立方体个数都会净增 7 个。因此,为了证明上面给出的结论,我们只需要构造出 n = 48, 49, 50, 51, 52, 53, 54 时的剖分方案即可。不过,究竟该怎么构造,这就要比刚才更有挑战性了。
n = 50 时的方案是最好构造的。从初始时的立方体出发,每次选一个小立方体并把它分成 8 份,于是我们便会得到 1 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 50 个小立方体。
把立方体分成 3 × 3 × 3 = 27 个小立方体,并把其中 8 个小立方体合成一个大立方体,我们便能得到 n = 20 时的方案,进而可以得到 20 + 7 + 7 + 7 + 7 = 48 个小立方体。在 n = 20 时的方案中选择一个小立方体,并套用这个方案本身把它细分成 20 份,我们便能得到 n = 39 时的方案,进而可以得到 39 + 7 + 7 = 53 个小立方体。
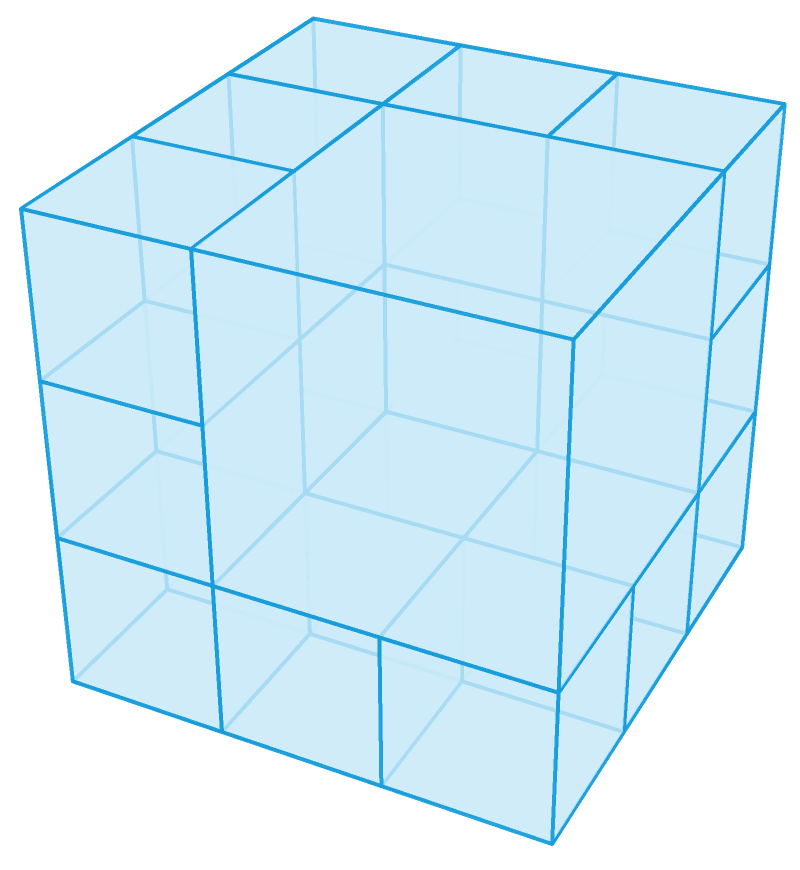
把立方体分成 4 × 4 × 4 = 64 个小立方体,并把其中 27 个小立方体合成一个大立方体,我们便能得到 n = 38 时的方案,进而可以得到 38 + 7 + 7 = 52 个小立方体。
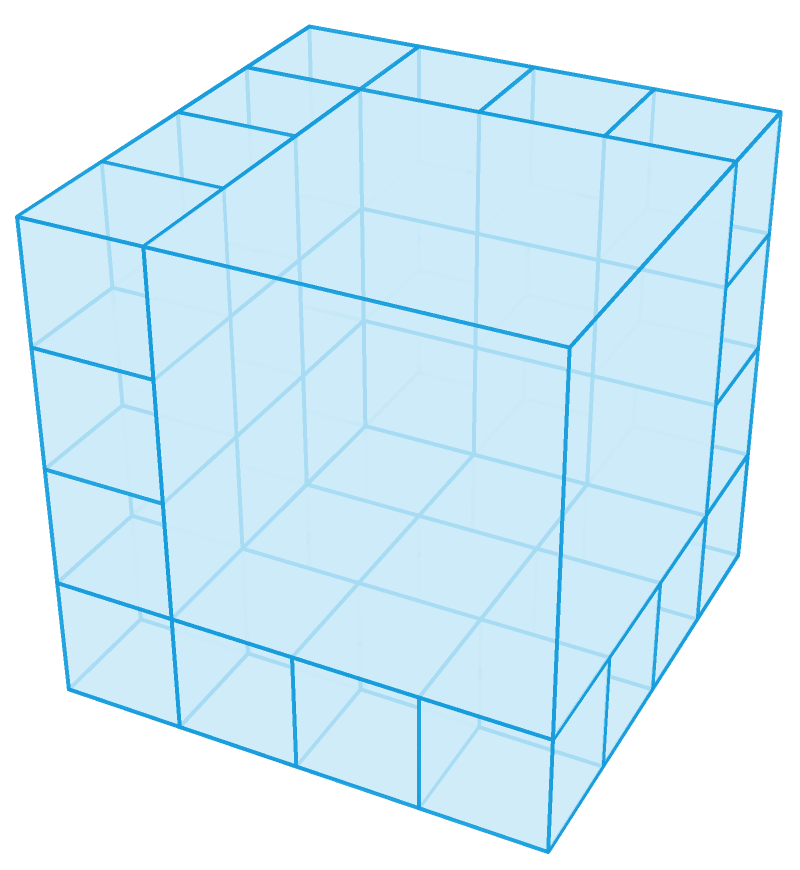
真正比较困难的就是构造 n = 49, 51, 54 时的方案了。前面的几个构造或多或少地都借鉴了正方形剖分问题的解法。利用这些构造,我们可以从初始时的 1 个立方体出发,不断地执行加 7 、加 19 、加 26 、加 37 四种操作之一。然而,这无论如何也变不出 n = 49, 51, 54 时的方案。因此,我们需要另辟蹊径。 n = 49 时的方案如下,它里面有 4 个边长为 1/2 的立方体, 9 个边长为 1/3 的立方体,以及 36 个边长为 1/6 的立方体。
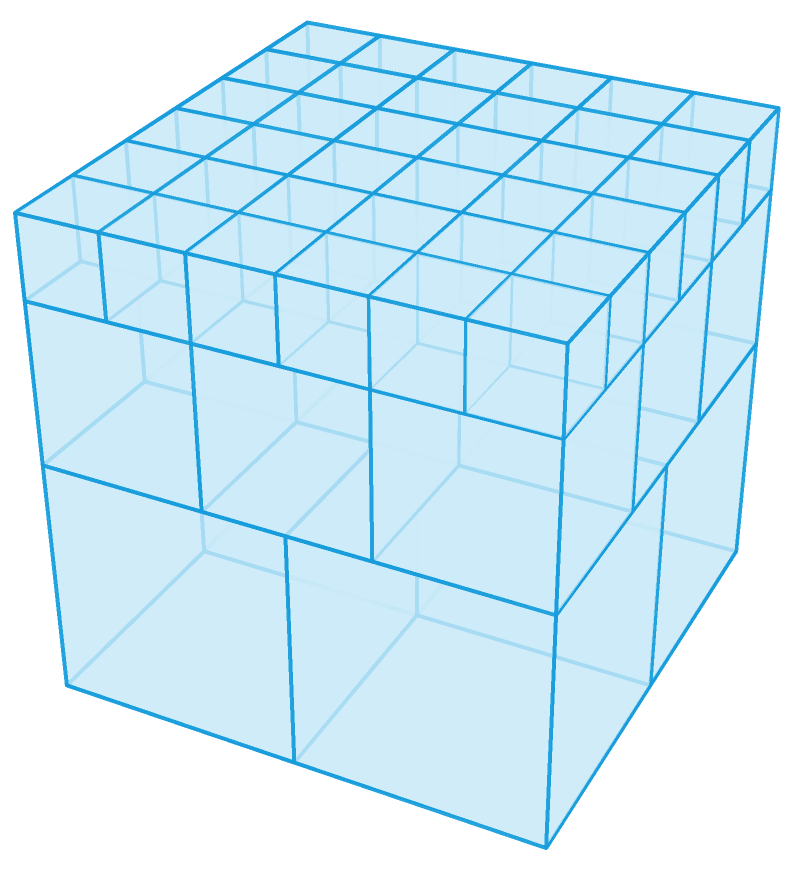
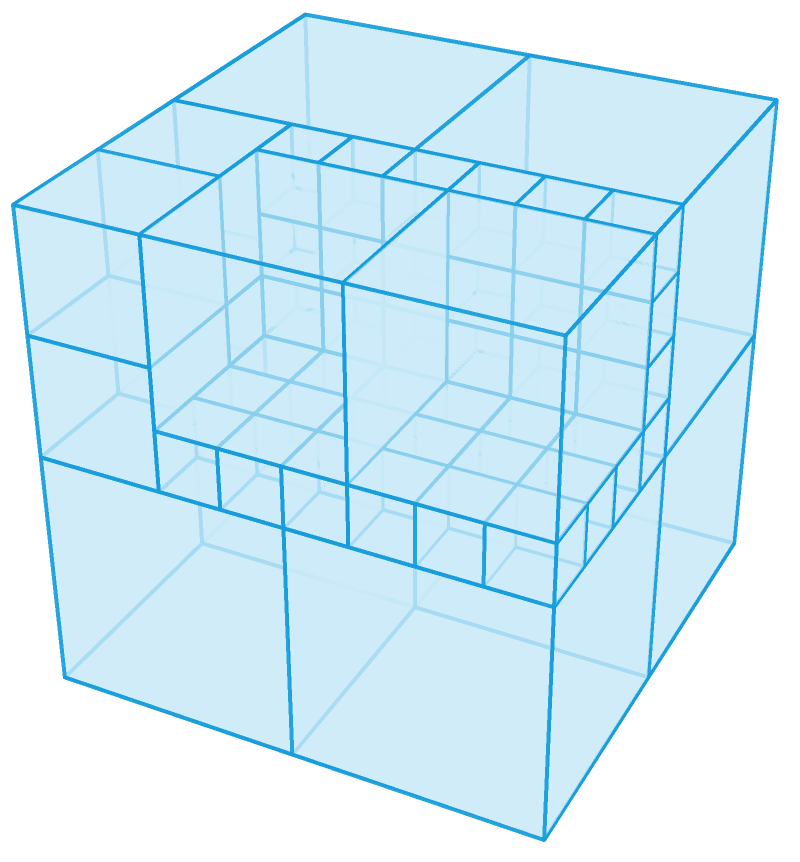
n = 51 时的方案如下,它里面有 5 个边长为 1/2 的立方体, 5 个边长为 1/3 的立方体,以及 41 个边长为 1/6 的立方体。
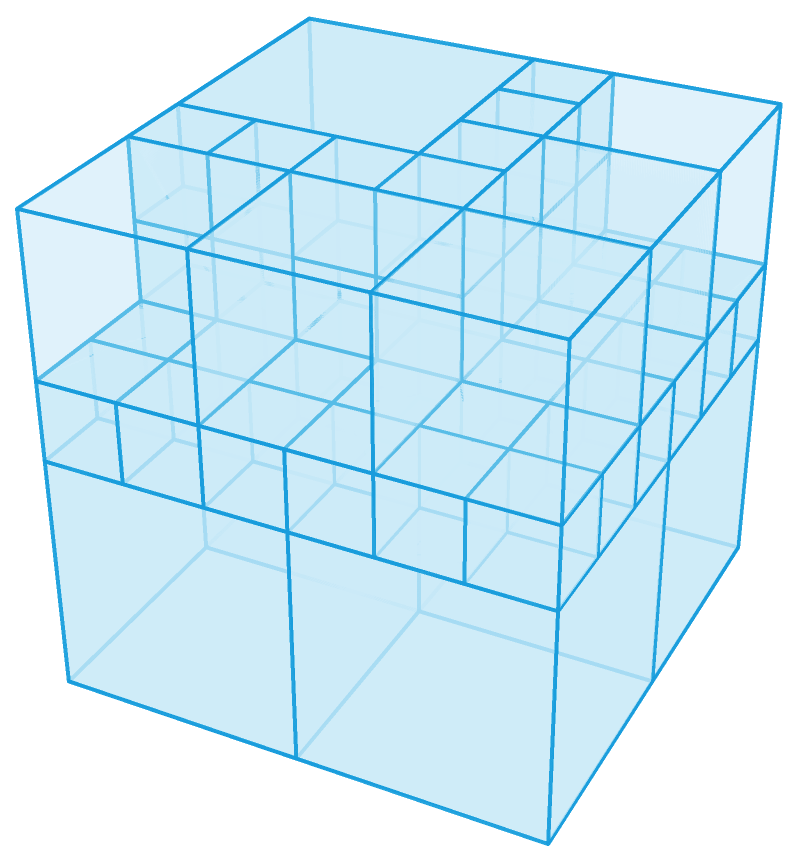
n = 54 时的方案最为复杂,很长一段时间里,人们甚至认为这样的方案根本不存在。但是最终,它还是被构造出来了。它里面有 2 个边长为 3/8 的立方体, 4 个边长为 1/4 的立方体, 6 个边长为 1/2 的立方体,以及 42 个边长为 1/8 的立方体。
至此,我们就完整地证明了,对于所有的 n ≥ 48 ,满足要求的立方体剖分方案都是存在的。
显然,这个问题还可以进一步扩展到更高维的空间。对于任意正整数 d ≥ 2 ,我们都可以问:能否找到某个正整数,使得对于所有大于等于该正整数的 n ,把 d 维立方体分割成 n 个小的 d 维立方体的方案都是存在的?如果能找到这样的正整数的话,那么这样的正整数最小是多少?不妨把这个最小的满足要求的正整数记作 c(d) 。我们现在已经知道了, c(2) 等于 6 ,并且 c(3) 很可能等于 48 。
容易证明,不管 d 是多少, c(d) 一定都是存在的。首先,我们来证明一个经典的数论结论:若 a 和 b 是两个互质的正整数,则对于所有的正整数 n ≥ a · b ,我们都能找到适当的非负整数 p 和 q ,使得 n = p · a + q · b 。
注意到,对于任意一个正整数 n ≥ a · b 都有, n, n – a, n – 2 · a, n – 3 · a, …, n – (b – 1) · a 是 b 个不同的正整数,并且它们除以 b 的余数互不相同。它们是 b 个不同的正整数,这很容易看出;但是,它们除以 b 的余数为什么互不相同呢?这是因为,如果存在 0 ≤ i < j ≤ b – 1 使得 n – i · a 和 n – j · a 除以 b 的余数相同,这就说明 n – i · a 和 n – j · a 之差是 b 的倍数,即 j · a – i · a = (j – i) · a 是 b 的倍数。既然 a 与 b 互质,要想让 (j – i) · a 是 b 的倍数,必然得让 j – i 是 b 的倍数。但是, i 和 j 都是 0 到 b – 1 之间的数,因而 j – i 比 b 要小,它不可能是 b 的倍数,于是产生矛盾。
然而,除以 b 的余数只有 b 种不同的可能。这说明, n, n – a, n – 2 · a, n – 3 · a, …, n – (b – 1) · a 除以 b 的余数取遍了所有的可能。因此,我们必然能找到某个 0 ≤ p ≤ b – 1 ,使得 n – p · a 除以 b 的余数为 0 ,即 n – p · a 是 b 的整倍数。这样一来, n 就正好能被表示成 p · a + q · b 了。
回到立方体剖分的问题。从初始时的立方体出发,每次把一个小立方体分割成 2d 个更小的立方体,整个剖分方案中的立方体个数都会净增 2d – 1 个;每次把一个小立方体分割成 (2d – 1)d 个更小的立方体,整个剖分方案中的立方体个数都会净增 (2d – 1)d – 1 个。因此,当 n 为任何一个形如 1 + p · (2d – 1) + q · ((2d – 1)d – 1) 的数时(其中 p 、 q 均为非负整数),剖分方案都是存在的。然而, 2d – 1 和 (2d – 1)d – 1 显然是两个互质的数(前者的某个整倍数与后者相差 1 ),由刚才的数论结论立即可得,对于所有的 n > (2d – 1)((2d – 1)d – 1) ,剖分方案都是存在的。
但是,对于更大的 d , c(d) 的值具体是多少,这仍然是数学当中的未解之谜。
这个问题最早是 1946 年由 N. J. Fine 和 I. Niven 在 The American Mathematical Monthly 上提出的,题目编号为 E724 。 Fritz Herzog 、 William Scott 、 Doris Rychener 、 Christoph Meier 、 Matthew Hudelson 都对问题的解答有不同程度的贡献。 Martin Gardner 在 Fractal Music, Hypercards and More: Mathematical Recreations from Scientific American Magazine 一书中指出 c(3) 的值就是 48 ,并列出了所有不满足要求的 n 值:
2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 16, 17, 18, 19, 21, 23, 24, 25, 26, 28, 30, 31, 32, 33, 35, 37, 40, 42, 44, 47
这一说法的来源不明。