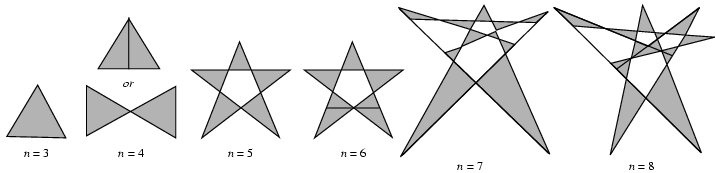
很多时候，问题越是简单，解答起来越复杂。1983年，Kobon Fujimura提出了这样一个问题：N条直线最多可以构成多少个互不重叠的三角形？这个问题后来被称为Kobon三角形问题。虽然对于一些特殊的n，人们已经找到了确切的最优解，但目前Kobon三角形问题还没有一般的结论。就在上个月，Johannes Bader用17条直线构造出85个互不重叠的三角形，它被证明是n=17的最优解。这里，我们将给出Johannes Bader构造出来的图形，并且证明它确实是n=17时的最优解。

      
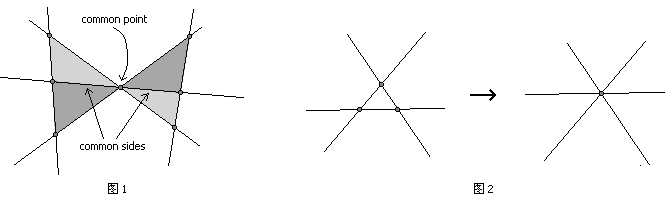
    如果n条直线中任两条不平行，任三条不共点，则每条直线都被其它n-1条直线切割为n份，产生了n-2个小线段，因此n条直线最多可以构成n(n-2)个小线段。我们将证明，n(n-2)/3是Kobon三角形问题的一个上界。有人会说，这不是显然的吗，如果这n(n-2)个小线段被“充分利用”的话，每条小线段都是一个三角形的边，n(n-2)/3显然已经是最大的了。且慢，万一两个三角形有公共边咋办？这样是不是可以“节约”一条边出来？有人甚至会想到，这样做节约的可不止一条边，如果两个三角形有公共边的话，必然会出现三线共点的情况，这将导致这两个三角形对面又产生另一对共边的三角形（图1）。但事实上，允许公共边的出现不但没有节约任何边，反而浪费了更多的线段。别忘了，三线共点这一情况的出现将减少总线段数，此时总线段数不再是n(n-2)，你将白白损失三条本该有所作为的线段（图2）。省了两条，丢了三条，可见同样是想构造n(n-2)/3个三角形，只要有共用边出现，n(n-2)条小线段是不够的。证明的基本思路就是这样，有兴趣的话大家可以自己整理出详细的证明过程。
    注意这个证明并没有说存在公共边的构造肯定不是最优解。有可能对于某些n，某个包含公共边的解是最优解，只是它没达到这里给出的上界而已。另外大家可能会问到的问题是，是否存在“部分公共边”的情况。这种“大边包含小边”式的共边三角形显然是愚蠢的，因为此时其中一个三角形必然被划分为了更小的三角形，选择小的那个三角形显然更好。

    当n=17时，上界n(n-2)/3是可以达到的。Johannes Bader构造出了下面这个图形，图形中包含了85个互不重叠的三角形，完美解决了n=17时的Kobon三角形问题。

查看更多：http://www.tik.ee.ethz.ch/sop/people/baderj/?page=other.php
做人要厚道，转贴请注明出处